Si dicono prodotti notevoli alcuni prodotti tra polinomi per i quali non è necessario applicare tutti i passaggi della proprietà distributiva, ma si assume come regola risolutiva l'ultimo passaggio di tale applicazione.
- Trinomio
- Quadrato del primo
- Quadrato del secondo
ESPRESSIONI CON I PRODOTTI NOTEVOLI
Per risolvere le espressioni algebriche in cui sono presenti prodotti notevoli si seguono le stesse procedure relative ala proprietà delle parentesi e delle operazioni.
E' obbligatorio risolvere applicando le regole sui prodotti notevoli.
Il quadrato di un binomio è uguale ad un trinomio costituito dal quadrato del primo termine, dal quadrato del secondo termine, dal doppio prodotto del primo termine per il secondo termine applicando la regola del segno.
2. SOMMA PER DIFFERENZA
Il prodotto di un binomio somma per il binomio differenza cioè un binomio per un secondo binomio in cui un monomio resta uguale anche nel segno ed nel secondo monomio cambia soltanto il segno cioè un monomio differenza costituito dal prodotto dei monomi simili applicando la regola del segno.
3. QUADRATO DI UN POLINOMIO
Il quadrato di un polinomio è uguale ad un polinomio costituito dal quadrato di ciascun monomio e dal doppio prodotto di ogni monomio per il successivo.
Applicando la regola del segno.
4. CUBO DI UN BINOMIO
Il cubo di un binomio è uguale ad un quadrinomio costituito dai cubi dei due termini, dal triplo prodotto del quadrato del primo termine per il secondo senza quadrato, dal triplo prodotto del primo termine senza quadrato per il secondo al quadrato.
Applicando la regola dei segni.
( x + y )³ = x³ + 3x3y + 3xy3 + y3
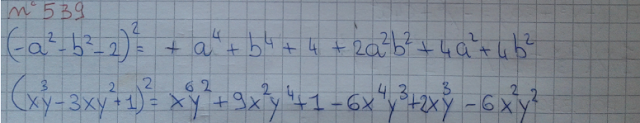
Nessun commento:
Posta un commento